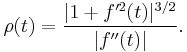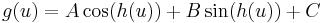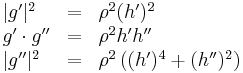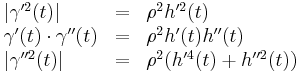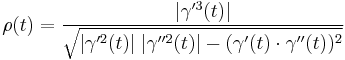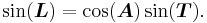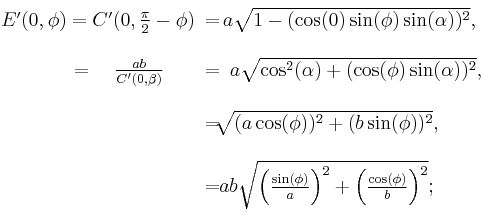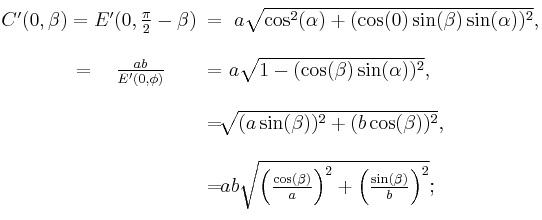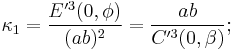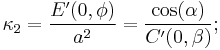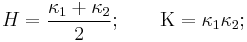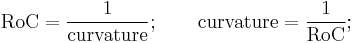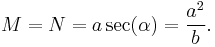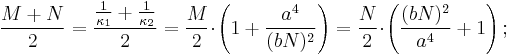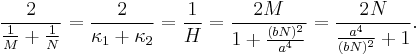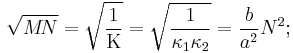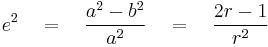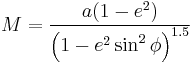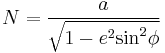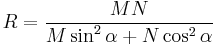Radius of curvature (applications)
The distance from the center of a circle or sphere to its surface is its radius. For other curved lines or surfaces, the radius of curvature at a given point is the radius of a circle that mathematically best fits the curve at that point.
The equivalent "surface radius" that is described by radial distances at points along a body's surface is its radius of curvature (more formally, the radius of curvature of a curve at a point is the radius of the osculating circle at that point). With a sphere, the radius of curvature equals the radius. With an oblate ellipsoid (or, more properly, an oblate spheroid), however, not only does it differ from the radius, but it varies, depending on the direction being faced. The extremes are known as the principal radii of curvature.
Contents |
Explanation
Imagine driving a car on a curvy road on a completely flat plain (so that the geographic plain is a geometric plane). At any one point along the way, lock the steering wheel in its position, so that the car thereafter follows a perfect circle. The car will, of course, deviate from the road, unless the road is also a perfect circle. The radius of that circle the car makes is the radius of curvature of the curvy road at the point at which the steering wheel was locked. The more sharply curved the road is at the point you locked the steering wheel, the smaller the radius of curvature.
Formula
If 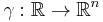 is a parameterized curve in
is a parameterized curve in 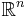 then the radius of curvature at each point of the curve,
then the radius of curvature at each point of the curve, 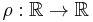 , is given by
, is given by
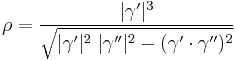 .
.
As a special case, if f(t) is a function from  to
to  , then the curvature of its graph,
, then the curvature of its graph, 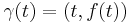 , is
, is
Derivation
Let  be as above, and fix
be as above, and fix  . We want to find the radius
. We want to find the radius  of a parameterized circle which matches
of a parameterized circle which matches  in its zeroth, first, and second derivatives at
in its zeroth, first, and second derivatives at  . Clearly the radius will not depend on the position (
. Clearly the radius will not depend on the position (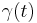 ), only on the velocity (
), only on the velocity (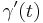 ) and acceleration (
) and acceleration (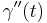 ). There are only three independent scalars that can be obtained from two vectors v and w, namely v·v, v·w, and w·w. Thus the radius of curvature must be a function of the three scalars
). There are only three independent scalars that can be obtained from two vectors v and w, namely v·v, v·w, and w·w. Thus the radius of curvature must be a function of the three scalars 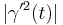 ,
, 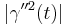 and
and 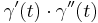 .
.
The general equation for a parameterized circle in 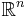 is
is
where 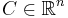 is the center of the circle (irrelevant since it disappears in the derivatives),
is the center of the circle (irrelevant since it disappears in the derivatives), 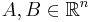 are perpendicular vectors of length
are perpendicular vectors of length  (that is,
(that is, 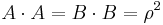 and
and 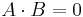 ), and
), and 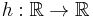 is an arbitrary function which is twice differentiable at t.
is an arbitrary function which is twice differentiable at t.
The relevant derivatives of g work out to be
If we now equate these derivatives of g to the corresponding derivatives of  at t we obtain
at t we obtain
These three equations in three unknowns ( ,
, 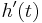 and
and 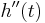 ) can be solved for
) can be solved for  , giving the formula for the radius of curvature:
, giving the formula for the radius of curvature:
or, omitting the parameter (t) for readability,
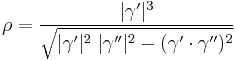 .
.
Elliptic, latitudinal components
The radius extremes of an oblate spheroid are the equatorial radius, or semi-major axis, a, and the polar radius, or semi-minor axis, b. The "ellipticalness" of any ellipsoid, like any ellipse, is measured in different ways (e.g., eccentricity and flattening), any and all of which are trigonometric functions of its angular eccentricity, 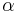 :
:
The primary parameter utilized in identifying a point's vertical position is its latitude. A latitude can be expressed either directly or from the arcsine of a trigonometric product, the arguments (i.e., a function's "input") of the factors being the arc path (which defines, and is the azimuth at the equator of, a given great circle, or its elliptical counterpart) and the transverse colatitude, which is a corresponding, vertical latitude ring that defines a point along an arc path/great circle. The relationship can be remembered by the terms' initial letter, L-A-T:
Therefore, along a north-south arc path (which equals 0°), the primary quadrant form of latitude equals the transverse colatitude's at a given point. As most introductory discussions of curvature and their radius identify position in terms of latitude, this article will too, with only the added inclusion of a "0" placeholder for more advanced discussions where the arc path is actively utilized: 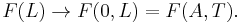 There are two types of latitude commonly employed in these discussions, the planetographic (or planetodetic; for Earth, the customized terms are "geographic" and "geodetic") and reduced latitudes,
There are two types of latitude commonly employed in these discussions, the planetographic (or planetodetic; for Earth, the customized terms are "geographic" and "geodetic") and reduced latitudes, 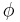 and
and 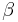 (respectively):
(respectively):
The calculation of elliptic quantities usually involves different elliptic integrals, the most basic integrands being 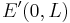 and its complement,
and its complement, 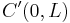 :
:
Thus 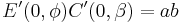 .
.
Curvature
A simple, if crude, definition of a circle is "a curved line bent in equal proportions, where its endpoints meet". Curvature, then, is the state and degree of deviation from a straight line—i.e., an "arced line". There are different interpretations of curvature, depending on such things as the planular angle the given arc is dividing and the direction being faced at the surface's point. What is concerned with here is normal curvature, where "normal" refers to orthogonality, or perpendicularity. There are two principal curvatures identified, a maximum, κ1, and a minimum, κ2.
Meridional maximum
- The arc in the meridional, north-south vertical direction at the planetographic equator possesses the maximum curvature, where it "pinches", thereby being the least straight.
Perpendicular minimum
- The perpendicular, horizontally directed arc contains the least curvature at the equator, as the equatorial circumference is——at least in mathematical definition——perfectly circular.
The spot of least curvature on an oblate spheroid is at the poles, where the principal curvatures converge (as there is only one facing direction——towards the planetographic equator!) and the surface is most flattened.
Merged curvature
- There are two universally recognized blendings of the principal curvatures: The arithmetic mean is known as the mean curvature, H, while the squared geometric mean——or simply the product——is known as the Gaussian curvature, K:
Principal radii of curvature
A curvature's radius, RoC, is simply its reciprocal:
Therefore, there are two principal radii of curvature: A vertical, corresponding to κ1, and a horizontal, corresponding to κ2. Most introductions to the principal radii of curvature provide explanations independent to their curvature counterparts, focusing more on positioning and angle, rather than shape and contortion.
Meridional radius of curvature
- The vertical radius of curvature is parallel to the "principal vertical", which is the facing, central meridian and is known as the meridional radius of curvature, M (alternatively, R1 or p):
-
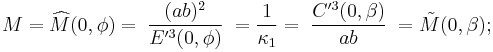
- (Crossing the planetographic equator,
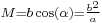 .)
.)
- (Crossing the planetographic equator,
Normal radius of curvature
- The horizontal radius of curvature is perpendicular (again, meaning "normal" or "orthogonal") to the central meridian, but parallel to a great arc (be it spherical or elliptical) as it crosses the "prime vertical", or transverse equator (i.e., the meridian 90° away from the facing principal meridian——the "horizontal meridian"), and is known as the transverse (equatorial), or normal, radius of curvature, N (alternatively, R2 or v):
-
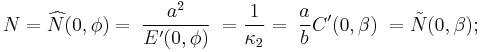
- (Along the planetographic equator, which is an ellipsoid's
- only true great circle,
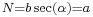 .)
.)
Polar convergence
- Just as with the curvature, at the poles M and N converge, resulting in an equal radius of curvature:
-
Merged radius of curvature
- There are two possible, basic "means":
-
-
- Mean radius of curvature, which is the arithmetic mean:
-
-
-
- Radius of mean curvature, which is the harmonic mean:
-
- If these means are then arithmetically and harmonically averaged together, with the results reaveraged until the two averages converge, the result will be the arithmetic-harmonic mean, which equals the geometric mean and, in turn, equals the square root of the inverse of Gaussian curvature!
- While, at first glance, the squared form may be regarded as either the "radius of Gaussian curvature", "radius of Gaussian curvature2" or "radius2 of Gaussian Curvature", none of these terms quite fit, as Gaussian Curvature is the product of two curvatures, rather than a singular curvature.
Applications and examples
- For the use in differential geometry, see Cesàro equation.
Radius of curvature is also used in a three part equation for bending of beams.
Radius of curvature on the Earth
This section gives the formulas needed to calculate the radius of curvature of the spheroid used to approximate the surface of the Earth. The notation used in this section may or may not agree with that used in the rest of the article.
Specifying the spheroid
Numerous spheroids have been used in the past to approximate the Earth's surface; each of them is defined by two numbers. Usually one is  , the distance from the center of the spheroid to the equator; the second may be
, the distance from the center of the spheroid to the equator; the second may be  , the slightly-smaller distance from the spheroid center to the pole, or it may be the dimensionless number
, the slightly-smaller distance from the spheroid center to the pole, or it may be the dimensionless number  expressing the difference between the two spheroid dimensions
expressing the difference between the two spheroid dimensions
-
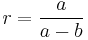 (
( 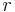 is also known as
is also known as 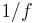 , the reciprocal of the flattening)
, the reciprocal of the flattening)
For the WGS84 spheroid, now commonly used,  is set to be 6378137 meters exactly and
is set to be 6378137 meters exactly and  is set to be 298.257223563 exactly (which makes
is set to be 298.257223563 exactly (which makes  about 6356752.3142 meters).
about 6356752.3142 meters).
Another dimensionless number is 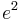 , the eccentricity squared of the spheroid
, the eccentricity squared of the spheroid
(Irrelevant aside: if we look at a cross-sectional ellipse containing the spheroid's pole-to-pole axis, the eccentricity  is the distance from the center of the ellipse to a focus, divided by
is the distance from the center of the ellipse to a focus, divided by  , the longer half-axis of the ellipse. In other words, if the eccentricity of an ellipse is 0.5, each focus is halfway from the center of the ellipse to its end.)
, the longer half-axis of the ellipse. In other words, if the eccentricity of an ellipse is 0.5, each focus is halfway from the center of the ellipse to its end.)
Formulas
At any given point on the spheroid, a vertical plane is a plane containing the vertical line through that point; we're going to pretend that the vertical line is the line perpendicular to the surface of the spheroid at that point. (On the real earth that isn't quite right, but it's just a semantic error; the line that's perpendicular to the spheroid surface exists, and calling it "vertical" is easier than calling it something else that would be strictly correct.)
If we cross-section the spheroid with a vertical north-south plane, the radius of curvature of the resulting ellipse at latitude 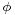 is
is
The radius of curvature of the ellipse cross-sectioned by a vertical east-west plane through a point at latitude 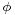 is
is
(Irrelevant aside: N is also the distance from the point to the spheroid's axis, measured along the straight line that is vertical at the point.)
Another of Euler's many formulas gives the radius of curvature of the ellipse cross-sectioned by a vertical plane in some direction other than north-south or east-west
where  is the azimuth of the line at the point: north equals zero, east equals 90 degrees. At the pole M = N, but at any other point M is the minimum radius of curvature of all the possible vertical cross-sections through that point, while N is the maximum.
is the azimuth of the line at the point: north equals zero, east equals 90 degrees. At the pole M = N, but at any other point M is the minimum radius of curvature of all the possible vertical cross-sections through that point, while N is the maximum.
See also
|
External links
- USIGS Glossary (Definitions of "transverse" terms)
- The Geometry Center: Principal Curvatures
- 15.3 Curvature and Radius of Curvature
- Weisstein, Eric W., "Principal Curvatures" from MathWorld.
- Weisstein, Eric W., "Principal Radius of Curvature" from MathWorld.
|
||||||||||||||